Стан и намаляване функция

Определяне нарастваща функция.

функция у = F В (х) се увеличава X. интервала ако за всяка неравенството. С други думи - най-голямата стойност на аргумента съответства на по-голяма стойност на функцията.

Определяне намаляваща функция.

функция у = F В (х) намалява X. интервала ако за всяка неравенството. С други думи - най-голямата стойност на аргумента съответства на минималната стойност на функцията.

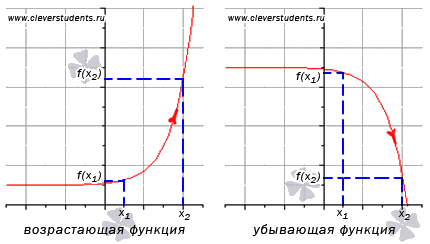
Забележка: Ако функцията се определя и непрекъснато в крайните точки на спускането на интервал или възходящ (А; б). т.е. при х = а и х = б. тези точки са включени в периода на възходящ или низходящ ред. Това не противоречи на определения за увеличаване и намаляване на функциите на X.

Например, основните свойства на елементарните функции, които знаем, че у = sinx определени и непрекъснато за всички валидни стойности на аргумента. Следователно, увеличаването на движещ се функция в интервала може да се каже за увеличението на сегмента.

Екстремум точки, екстремни функции.

Точка се нарича максимум функция у = е (х). ако за всички х в неравенството квартал. Стойността на функция при максималната точка nazyvayutmaksimumom функцията и етикета.

Точка се нарича минимална точка на функция у = F (х). ако за всички х в неравенството квартал. Стойността на функция на минималната функцията точка nazyvayutminimumom и етикета.

Под квартал разбере интервал, където - е достатъчно малка, за положително число.

Точка минимален и максимален брой точки, се наричат ​​крайни. и стойностите на функцията съответстваща на екстремум точки, наречени крайностите на функции.

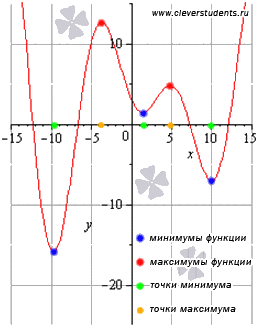
Не бъркайте екстремумите на функцията с най-високата и най-ниската стойност на функцията.

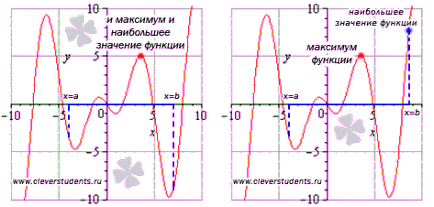
В първата цифра най-голямата функция стойност на интервала [а, Ь] се постига максималната точка и е равна на максимума на функцията, а втората цифра - максималната стойност се постига в точка х = б. който не е с максимална точка.

Достатъчни условия за увеличаване и намаляване на функции.

Въз достатъчни условия (атрибути) на нарастване и намаляване функции са интервали от увеличаване и намаляване функции.

Ето текстът на признаци за увеличаване и намаляване на функция в интервала:

ако производното на функция у = F (х) е положително за всички х от увеличава функция X. интервал от X;

ако производното на функция у = F (х) е отрицателна за всички х от интервала на функция X. намалява в X.

По този начин, за да се определи интервалите на увеличаване и намаляване функция трябва да:

намерете домейна на функцията;

намерите производно на функцията;

решаване на неравенството и на домейна;

добави в резултат пропуски граница точката, при която функцията е дефинирана и непрекъсната.

Вземем примера на констатация за увеличаване на интервалите и намаляване на функцията, за да обясни на алгоритъма.

Намери интервали от увеличаване и намаляване функция.

Първата стъпка е да се намери дефиниция на функция за придобиване. В нашия пример, изразът в знаменателя не става нула, следователно.

Ние се обръщаме към намиране на производна на функция:

За определяне на интервалите на увеличаване и намаляване през достатъчна база функция решаване на неравенства и на домейна. Ние използваме обобщение на интервал метод. Единствената корените на числителя е х = 2. и знаменателят става нула при х = 0. Тези точки разделят домен в интервали, в която производното запазва подпише. Имайте предвид следните точки на редица линия. Тънкостите обикновено означават интервали за което производното е положителна или отрицателна. Стрелките долу схематично показват увеличаване или намаляване на функцията на подходящ интервал.

По този начин, и двете.

В точка х = 2, функцията се определя и непрекъснато, но това трябва да се добави в процепа за увеличаване и намаляване на разликата. В точката х = 0 не е определена, следователно, не включват тази точка в желаните интервали.

Тук е функцията за график за сравнение с тях резултати.

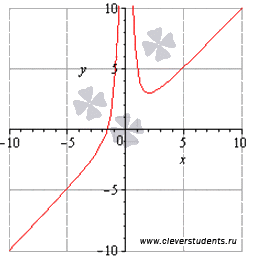
функция се увеличава с намаляване на интервала (0, 2].