Комплекс за движение на точка теорема на Кориолис
Определяне на комплекс (композитен) движение на точката. Определяне на абсолютната, относителна и преносим движение, скоростта и ускорението. Доказателството за добавяне на цени теорема и добавяне на Кориолис ускорения. Кориолис (въртене) ускорение.
Тук ние показваме, че сложната движение, абсолютната скорост на точка е векторна сума от относителните скорости и преносим:
.
Абсолютната точка ускорение е равна на сумата вектор на относителната, преносими и Кориолис (въртене) ускорението:
,
където - Кориолис ускорение.
Пример за приложение на теорията представени по-долу е даден на страница "Сложно движението на точката. Един пример за решаването на проблема. "
Комплекс (композитен) движение на точката
случаите, когато точка изпълнява известни движение по отношение на твърдо тяло често се срещат. Такъв орган, който от своя страна, се движи по отношение на фиксираната координатна система. И движението на една точка по отношение на тялото, а правото на движение на тялото по отношение на фиксираната координатната система, са известни или са определени. Задължително да намерите най-кинематични количества (скорост и ускорение) на върха по отношение на фиксирана координатна система.
Такова движение на точката се нарича комплекс или съединение.
Комплекс или композитен движение на точка - движението в движението координатна система. Това означава, че движението на точки, описани в координатната система, която от своя страна е в движение по отношение на фиксираната координатна система.
Освен това, за по-голяма яснота, ние ще приемем, че преместването координатна система, неподвижно свързана с някои твърдо тяло. Ще разгледаме движението на точката спрямо тялото (относителното движение) и движението на тялото по отношение на фиксирана координатна система (постъпателно движение).
Относителният движението на една точка в комплекс движение - движението на тялото по отношение на точката (преместването координатна система) Като се има предвид, че тялото почива.
Преносим движение на точка в комплекс движение - точка движение неподвижно свързан тяло, причинени от движението на тялото.
Абсолютната движение на точка в комплекс движение - една точка на движение във връзка с фиксирана координатна система, причинени от движението на тялото и движение на върха по отношение на тялото.
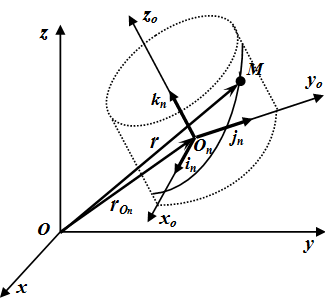
Комплекс движение. Точката М се движи спрямо движещото се тяло.
Нека Oxyz - фиксирана координатна система, XO йо зо - движещ се координатна система, неподвижно свързана с тялото. Нека - вектори единица (базисни вектори), насочени по XO оста. йо. Zo придвижване координатна система. Тогава радиус вектор от точка М в неподвижната система се получава от:
(1)
при което - радиус вектор от точка - започне да се движи координатна система, прикрепена към тялото.
Относителната скорост и ускорение
При смяна на относителното движение координира XO. йо. ZO точка спрямо тялото. А вектори са постоянни, независимо от времето. Разнообразяване на (1) по отношение на времето, като се приема постоянно, ние получаваме формулата за относителната скорост и ускорение:
(2);
(3).
Относителната скорост на точка в комплекс движение - е скоростта, с фиксирана точка на положението на тялото (преместването координатна система), причинени от движението на точка спрямо тялото.
Относително ускорение в точката на комплекс движение - тази точка ускорение на определена позиция на тялото, причинено от движението на точка спрямо тялото.
Транслиращи скорост и ускорение
Когато преносими векторите на движението са се променили. определяне на положението на тялото. Относителни координати на точка ХО. йо. зо са постоянни. Разнообразяване на (1) по отношение на времето, като се предполага оксо. йо. зо постоянно, ние получаваме формули за преносими скорост и ускорение:
(4);
(5).
Преносим скорост точка когато комплекс движение - е скоростта на точка неподвижно закрепена към тялото, причинено от движението на тялото.
Преносим точка ускорение за комплекс движение - е ускоряване точка неподвижно закрепена към тялото, причинено от движението на тялото.
производно време на - скоростта и ускорението на произхода на движещите се координатна система On. ;.
Формули за време производни на вектори. Вземаме две произволни точки на твърди тела А и В. Тези скорости са свързани с:
(Вж. Page "Скоростта и ускоряване на твърда точки тяло"). Помислете вектора. съставен от точка А до точка В. След
.
Разграничаване по отношение на времето и прилагат предишната формула:
.
Така че сме намерили формулата за времето производна на вектора, свързващ две точки на тялото:
.
Тъй като векторите са здраво свързани с тялото, техните производни време се определят от тази формула:
(6).
Заместването в (4):
Така, изразът (4) води до формула за скоростта на твърди точки на тялото.
Чрез извършване на такова преобразуване на формула (5). Ние получи формула за ускорение Твърди точки:
,
където - ъглово ускорение на тялото.
Абсолютната скорост и ускорение
Ако абсолютната промяна на движението като вектори. определяне на позицията на тялото и относителните координатите на точка XO на. йо. зо.
Абсолютната скорост на точка в комплекс движение - е скоростта на точка в определена координатна система.
Absolute точка ускорение за комплекс движение - това ускорение точка в определена координатна система.
Теорема на добавяне на скорости
Когато абсолютната скорост на композитен точката на движение е равна на сумата от вектор относителната скорост и преносим:
.
доказателства
Разграничаване (1) по отношение на времето, като се използват правилата на диференциация на суми и продукти. Тогава заместител (2) и (4).
(1);
(7)
.
Кориолис теорема за добавяне на ускорения
Ако единичните точки за движение абсолютен ускорение е равна на сумата вектор на относителната, преносими и Кориолис (въртене) ускорение:
,
където
- Кориолис ускорение.
доказателства
Разграничаване (7) по отношение на времето, като се използват правилата на диференциация на суми и продукти. Тогава заместител (3) и (5).
(7).
Последният термин се прилага (6) и (2).