Ако височината на триъгълника са равни, тогава те са третирани като основния квадрат

№2 следствие на теоремата на площта на триъгълник

S1 е площта на триъгълника ABC
S2 е площта на триъгълника DEF

Свързани теми. Отворете материалите в отделни страници или раздели на браузъра

Като се има предвид два триъгълника и ΔAVS ΔDEF

В разгара на тези триъгълници са равни: BK = EH

AC и DF - базови триъгълници (тези страни са конструирани на височина)

означаваме:
S₁ - област ΔAVS
S₂ - област ΔDEF

Това е следствие казва, че истинско равенство:

Нека да видим, какъв е смисълът на тази формула.
Нека AC = 6 см и DF = 3 см, получаваме

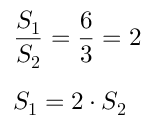
Т.е. ABC триъгълник е два пъти площта от триъгълника DEF

От теоремата на площта на триъгълник може да се запише формула областта на тези триъгълници:

BK = EH при условие, може да се запише:

Ние считаме, съотношението на областта на триъгълници (разделят една област в друга)