Вероятност 10

Средна raspredelenie.Funktsiya нормално разпределение. функция на Лаплас. Числени характеристики на нормалното разпределение. Вероятността от удари нормално разпределена случайна променлива в даден интервал. Три сигма владеят. Разпределенията, свързани с нормалното: разпределение на Стюдънт и Фишер Пиърс. Характерните функция на нормалното разпределение.

8.1. нормалната функция на разпределение

Един от най-разпространените дистрибуции е нормалното разпределение. Той играе важна роля в теорията на вероятностите и нейните приложения. Основната роля на нормалното разпределение, тъй като сумата от случайни величини с увеличаване на броя на мандатите в доста широки предположения държат асимптотично нормално (вж. "Централен Limit Теорема").

Плътността на функцията за нормално разпределение има формата

нормалната функция на разпределение има формата

Често, обаче, вместо нормалната функция на разпределение, като се използва функцията на Лаплас.

Нека а = 0,  = 1, получаваме

Такава функция се нарича стандартното нормално разпределение. Пишем тази функция в следния вид

.

Тъй F0 (+ ) = 1, тогава от симетрия, първият термин е равна на 0,5, а вторият е функцията на Лаплас

.

Следователно ние получаваме равенството

свързваща функция на нормалното разпределение и функцията на Лаплас.

Има широки маси за стандартното нормално разпределение и функцията на Лаплас. Въпреки това, той трябва да се има предвид, че понякога вместо обмислят функции с помощта на функцията

или функция грешка

Забележка. Откриване на нормално разпределение, свързани с имената на Гаус и Лаплас. в която се появява за първи път връзка с разследването на теорията на грешките, както и метода на най-малките квадрати. Ето защо, на нормалното разпределение се нарича още Гаусово разпределение, Лаплас. или просто Гаусово разпределение или Лаплас.

Ние считаме, очакването за нормално разпределение:

.

.

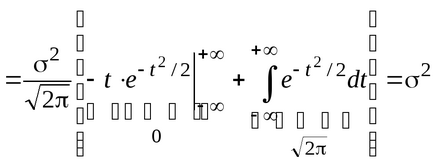
т.е. Нормално разпределение се характеризира с два параметъра: а. като чувство на очакване и , като чувство на стандартното отклонение.

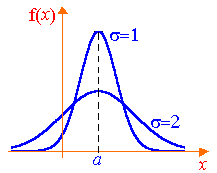
Графиката на функцията на нормално разпределение плътност има следната форма (Gaussian крива). Максимална е х = а. инфлексни точки в - и + . Кривата е симетрична по отношение на линия х = а. С намаляване на  крива става все по-високите си стойности.

8.2. Вероятността от удари нормално разпределена случайна променлива при предварително определен интервал

Известно е, че ако случайна променлива X е дефинирано разпределение плътност е (х), вероятността, че X приема стойността принадлежащи на интервала (, ), има формата

.

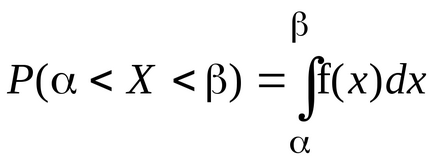
В случай на нормалното разпределение, тази формула се следната форма

Често е необходимо да се изчисли вероятността случайна променлива X отклонение в абсолютна стойност по-малко от предварително определена положително число , т.е. е необходимо да се намери вероятността за неравенството | X-а |<. Заметим, что неравенство равносильным ему двойным неравенством a –

.

По-специално, ако  г.

Последното равенство показва, че много практически въпроси при разглеждане на нормалното разпределение, можем да пренебрегнем възможността за отклонение от случайна променлива е по-голяма от 3 Това е т.нар изключи "три сигма".

Например, всеки, който се занимава с измервания, се срещна със ситуация, където има "див стойност." Във връзка с този проблем: Изключване на стойността, или трябва да бъде оставено. По този начин развитието на стандартно време за производство на едно парче направи следните измервания: 5,0; 4.8; 5.2; 5.3; 5.0; 6.1. Последният брой е много по-различна от другите. В тази връзка, възниква въпросът дали грешката е скрита в измерванията тук. Ние изчисляваме средната стойност

и средното квадратично otklonenie = 0.46. След това се конструира "trehsigmovy" интервал (4.84, 6.61). Тъй като стойността на х = 6,1 не се простира отвъд trehsigmovoy зона, тя не може да се разглежда като "дива".

Друг пример. На транспортна произведени части. Въз основа на елементи на статистически данни за мониторинг изчисляват средната квадратна otklonenie. След това се изгради директна средната линия, ресни trehsigmovoy лента. Ако точките на контролни измервания са в рамките trehsigmovoy банда, процесът трябва да се счита за стабилен и висококачествени продукти. Ако точките са близки до водещите линии, но не надхвърлят trehsigmovoy зона, това показва, раздор процес. Ако точката отвъд trehsigmovoy зона, това означава, че е налице брак.

Пример 8.1. Машина произвежда топки. Топката се счита за добре, ако диаметър топка отклонение Х от дизайна на абсолютната стойност е не повече от 0.7 mm. Ако приемем, че случайна променлива X е нормално разпределена със стандартно отклонение от 0.4 mm. определи какъв процент от наличните топки произвежда машина.

Следователно, устройството произвежда 92% от подходящи части.

8.3. Разпределение, свързани с нормалното

8.3.1. Разпределение Pearson ( 2 -distribution)

Нека независими случайни величини U1. U2. ..., Великобритания описва стандартното нормално разпределение: Ui = N (0,1). След разпределението на сумата от квадратите на тези стойности

Той призова  2 дистрибуция ( "хи-квадрат") свобода skstepenyami. Изрично, плътността на тази функция разпределение има формата

където

гама функция; по-специално,  (п + 1) = N.

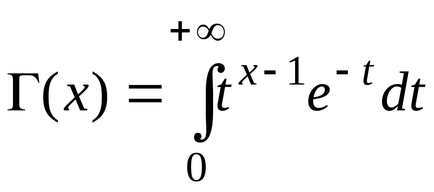
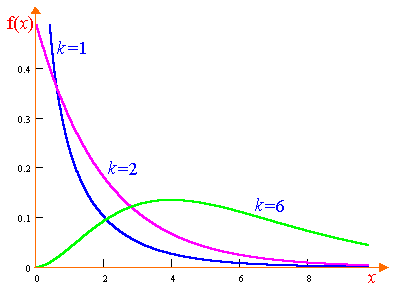
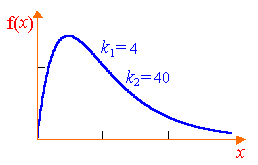
Pearson разпределение се определя от един параметър - броят на степените на свобода к. Графики на тази функция са показани на Фиг. 8.2. Числени характеристики на разпределението Pearson:

Ако случайни променливи  2 (К1) и  2 (К2) са независими, а след това

.

Имайте предвид, че с увеличаване на броя на степените на свобода Pearson разпределение постепенно се приближава нормално.

8.3.2. разпределение Student (т разпределение)

Да предположим, че U е стандартното нормално случайни променливи, U = N (0,1) и  2 - случайна променлива с  2 -distribution с к степени на свобода, където U и  две независими променливи. След разпределението на

Тя се нарича разпределение (т-разпределение), свобода skstepenyami Student. Изрично, плътността на функцията за разпределение на Стюдънт има формата

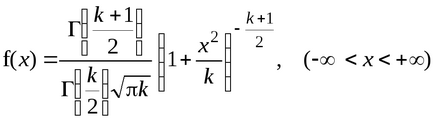
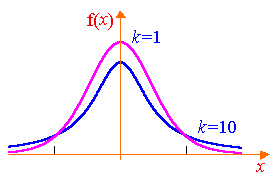
Графиката на тази функция е показана на Фиг. 8.3.

Числени характеристики на разпределението на Студентски:

Имайте предвид, че с увеличаване на броя на степените на свобода на разпределение Студентски бързо се приближава нормално.

8.3.3. Разпределение на Fischer (F-разпределение)

Нека  2 (К1) и  2 (К2) - независими случайни величини като  2 -distribution с съответно К1 и К2 степени на свобода. разпределението на

наречен Fisher разпределение (F-разпределение) sostepenyami svobodyk1ik2. Изрично Fisher плътност разпределение има формата

Графиката на тази функция е показана на Фиг. 8.4.

Числени характеристики на разпределението Fisher:

TMemo че между случайни променливи, които имат нормално разпределение, Pearson дистрибуция, Студентски и Фишър, ние имаме на отношенията:

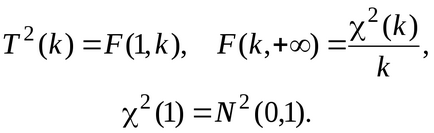
8.4 *. Характерните функция на нормалното разпределение

Нека случайна променлива  разпространявани от нормалното разпределение. След това ние получаваме за характерната функция

.

Осъществяване на промяната на у = х-IT. получаваме

.

От теорията на функциите на комплексна променлива е известно, че

.

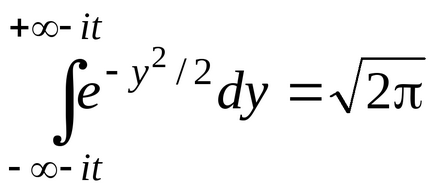
Затова ние най-накрая получи

.

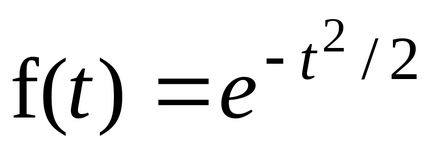
Както видяхме, ако случайна променлива  разпространявани от нормалното разпределение, а след това на случайна променлива  = t + m, но разпределени нормално закона с параметри м и . След това характерните черти f (т) и f (т) са свързани със свойството 2 от връзката

,

или най-накрая се получи, че характерната функция на нормалното разпределение е дадено от