Урок 3 матрица

Двигателят не се движи кораба. Корабът е все още на мястото си, а двигателят се движи Вселената във връзка с него. Futurama

Това е много важна част от урока, се уверете, че сте го прочетете няколко пъти и се разбира много добре.

До сега са работи за 3-измерни върховете например (X, Y, Z) триплети. Представяме друг параметър, w и ще работи на вектори на формата (X, Y, Z, W).

Помнете винаги, че:

• Ако w == 1, тогава вектора (X, Y, Z, 1) - позиция в пространството.
• Ако w == 0, векторът (X, Y, Z, 0) - тази посока.

Хомогенни координати ни позволява с едно математическа формула за работа с вектори, и в двата случая.

## Въведение в матрицата

Най-лесният начин за изпращане на матрица като масив от числа, с точно определен брой редове и колони. Например, 2x3 матрица, както следва:

Въпреки това, в триизмерни графики, ние просто ще се използва 4x4 матрица, която ще ни позволи да трансформираме връх (X, Y, Z, W). Трансформираната връх е резултат от умножението на матрица на самия връх:

** В горната част на матрица х (в този ред !!) = трансформира. ** връх

Доста проста. Ние ще го използват доста често, така че има смисъл да го повери на един компютър:

Опитайте се да експериментирате с тези фрагменти.

трансфер матрица изглежда така:

където X, Y, Z - ценности, които искате да добавите към нашия вектор.

Така че, ако искаме да се премести на вектора (10, 10, 10, 1) до 10 единици в посока на X, а след това ние получаваме:

... ние получаваме (20, 10, 10, 1) хомогенна вектор! Не забравяйте, че един в параметъра w, означава положението, но не и на посоката, както и трансформация ни не променя факта, че ние работим с позицията.

Сега си представете какво ще стане, ако векторът (0, 0, -1, 0) е линията:

... и да получите нашия оригинален вектор (0, 0, -1, 0). Както бе споменато по-рано, с вектора параметър w = 0 не може да се прехвърля.

И това е време, за да го преместите в кода.

** В GLSL. ** В действителност, никога няма да го направи в Shader, често ще изпълнява GLM :: превежда () в C ++, за да се изчисли на матрицата, да го прехвърля на GLSL, и вече е в Shader да се размножават:

Това е специална матрица, която не прави нищо, но ние я докосне, защото това е важно да се помни, че A се умножава по 1.0 дава A:

Тя изглежда толкова просто:

Така че, ако искате да приложите вектор мащабирането (позиция или посока - не е важно) до 2,0 във всички посоки, трябва да:

Имайте предвид, че w не се променя, както се обърне внимание на факта, че матрицата на идентичност - е специален случай на мащабиране матрица с фактор скала от 1 за всички оси. Също така матрицата на идентичност - е специален случай на матрицата за прехвърляне, където (X, Y, Z) = (0, 0, 0), съответно.

По-сложно, отколкото тези, които считат за по-рано. Ние пропусне данните тук, тъй като не е нужно да се знае със сигурност за ежедневна употреба. За повече информация, моля, кликнете върху линка и матрици Quaternions Често задавани въпроси (доста популярен ресурс и там може да има достъп до вашия език)

## Поставянето заедно преобразуването

Така че, сега ние сме в състояние да се върти, се движат и да приспособяваме вектори. Следващата стъпка би било добра идея да се съчетаят промяната, която се осъществява чрез следната формула:

ВНИМАНИЕ! Тази формула е в действителност показва, че мащабиране се извършва на първо място, а след това включете и само в краен случай, ако се движите. Ето как работи умножение на матрици.

Бъдете сигурни, да се запомни последователността, в която всичко това е направено, тъй като поръчката е наистина важно в крайна сметка, можете да го проверите сами:

• Вземете една стъпка напред и завий наляво
• Обърни се наляво и направи крачка напред

Разликата е наистина важно да се разбере, защото постоянно се сблъскват с това. Например, когато работите с героите от игра, или някои обекти, винаги е първо да се скала, след това включете и след това се прехвърля.

Размножаване на две матрици е много подобен на размножаването на матрици и вектори, така че ние се пропусне описанието, и ако искате да научите повече, отново можете да кликнете върху линка и матрици Quaternions FAQ.

До края на този урок, ние ще приемем, че ние знаем как да се покаже 3D модел на любимата си Blender - маймуна Сюзан.

World, видове и проекция матрица - е удобен инструмент за разделяне трансформации.

Този модел, както ни червен триъгълник определя от набор от върхове, чиито координати са дефинирани по отношение на центъра на обект, т.е.. Е. Vertex координатите (0, 0, 0) ще бъде в центъра на предмета.

На следващо място, ние бихме искали да се движат нашия модел, тъй като играчът контролира с помощта на клавиатурата и мишката. Всичко, което правим - това се отнася мащабиране, ротация, и след това се прехвърлят. Тези действия се извършват за всеки връх във всеки фрейм (извършва в GLSL, а не в C ++!) И по този начин нашият модел се движи на екрана.

Сега нашата връх в световната пространство. Това показва черната стрелка на фигурата. Ние са се преместили извън пространството обекта (всички върхове са определени по отношение на центъра на обекта) до Международната космическа (всички върхове са определени по отношение на централната част на света)

Схематично това е показано както следва:

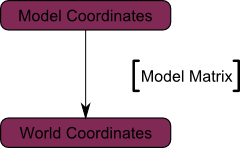
Отново цитирам Futurama:

Двигателят не се движи кораба. Корабът остава на същото място, както и двигателят се движи Вселената около него.

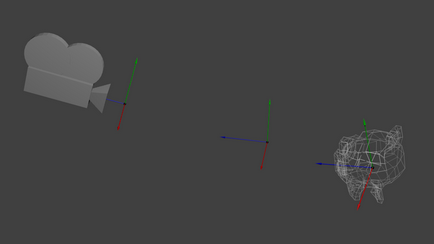
Опитайте се да си го представя във връзка с камерата. Например, ако искате да правите снимки на планината, вие не се движат на камерата, и да се премести в планината. Не е възможно в реалния живот, но това е изключително лесно в компютърната графика.

Така че, в началото, камерата се намира в центъра на света координатна система. За да преместите света, трябва да се въведе друга матрица. Да предположим, че искате да преместите камерата до 3 единици надясно (+ X), което е равно на движещи се по целия свят в 3 единици наляво (-X). В кода, то изглежда така:

Отново снимката по-долу показва това. Ние са се преместили от един свят, координатна система (всички върхове са определени по отношение на центъра на световната система) към камерата координатна система (всички върхове са определени по отношение на камерата):

Е, докато мозъкът ви го смила, ние гледаме на функцията, която ни дава GLM, а по-скоро на GLM :: LookAt:

Ето една графика, която показва това, което правим:

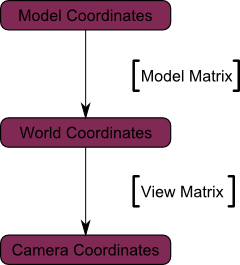
Така че сега ние сме в пространството на камерата. Това означава, че на върха на който ще получите координатите х == 0 и у == 0 ще се показва в центъра на екрана. Въпреки това, при показване на обекта също играе голяма роля за разстоянието на камерата (Z). За два възела със същия х и у, имащи по-голяма максимална стойност на Z ще се появи по-близо от друга.

Това се нарича перспектива проекция на:

И за щастие за нас, матрица 4x4 може да изпълнява тази proektsiyu¹:

Ние са се преместили от космоса камера (всички върхове са определени по отношение на камерата) в хомогенно пространство (всички върхове са в малък куб Всичко, което е вътре в куба. - се показва на екрана).

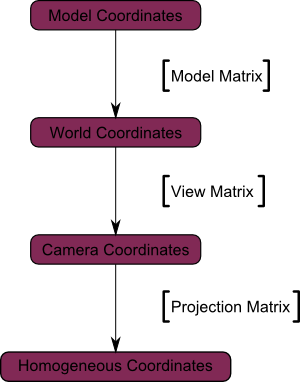
Сега погледнете следното изображение, така че можете да разберете по-добре какво се случва с проекцията. Преди проекцията имаме сините обекти в пространството на камерата, докато червената фигура показва преглед на камерата, това е. Е. Всичко това, което вижда камерата.

Използването на матрица проекция има следните реакции:

В този образ, преглед на камерата е куб, и всички обекти са деформирани. Обектите, които са по-близо до камерата изглеждат по-големи, а тези, които са по-далеч - малък. Също като в действителност!

Ето как ще изглежда:

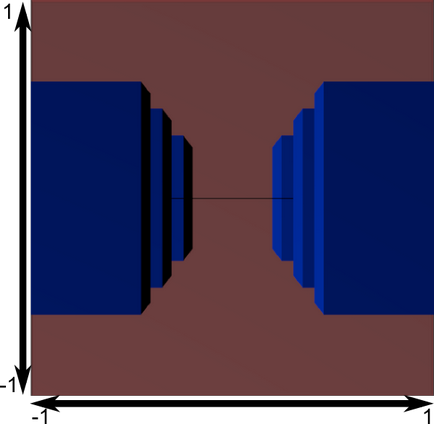
Изображението е квадрат, така че следната математическа трансформация се прилага за разтягане на изображението в зависимост от действителния размер на прозореца:

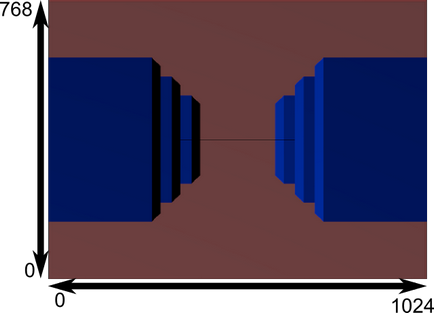
И този образ е това, което действително ще бъдат показани.

## Обединяване трансформация. ModelViewProjection матрица

... Само стандартните матрични преобразувания, които вече обичат!

• Първата стъпка - създаването на нашата MVP матрица. Това трябва да се направи за всеки модел, който да показвате.

• Втората стъпка - да предадат това в GLSL:

• Третата стъпка - да използват данните, получени в GLSL, за трансформиране на нашите върхове.

• Готово! Сега имаме един триъгълник, както е в Урок 2, все още се намира в основата (0, 0, 0), но сега можем да го видим в дългосрочен план от гледна точка (4, 3, 3).

В Урок 6, ще се научите как да променяте тези стойности динамично с помощта на клавиатурата и мишката, за да се създаде фотоапарат, който сте използвали, за да видите в игри. Но първо, ние се учим как да се даде този цвят модел (Урок 4) и текстура (Урок 5).

• Опитайте се да промените стойностите GLM :: перспектива
• Вместо да се използват перспектива прогнозен, се опита да използва ортогонална (GLM: орто)
• Променете ModelMatrix за превод, ротация и мащабиране на триъгълника
• Използване на предишната работа, но с различна последователност на операциите. Обърнете внимание на резултата.