Свойства на числата 1
Всъщност, всеки елемент подмножество dannogoelementnogo комплект съответства на един и само един елемент подмножество на същия набор.
Наистина, ние можем да изберем подмножество от елементи по следния начин: поправка елемент, номер елемент подгрупи, съдържащи този елемент, както и; номер елемент подгрупи, които не съдържат този елемент, както добре.
триъгълник на Паскал
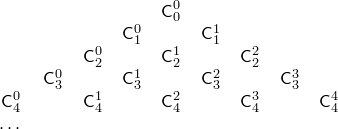
В този триъгълник, екстремните числата във всеки ред е равен на 1, а всеки, не е екстремно брой е сумата на две числа от предишния ред, стоящи над него. По този начин, на триъгълника ни позволява да се изчисли броят.

.
Доказателство. Помислете за набор от елементи и решаване на следния проблем по два начина: колко може да направи izelementov последователности от снимачната площадка, във всеки от които нито един елемент се среща два пъти?
1 начин. Изборът на първия срок на последователността, след втората, третата и т.н. член
2 метод. Ние избираме първите елементи на даден набор, а след това да ги подредите в някакъв ред
Размножава числителя и знаменателя на тази фракция от:
Пример. Колко начини може да бъде в играта, "Спорт Тото", за да изберете 5 номера от 36?
Необходимият брой начини
36 Понятието за случайни събития, вероятността на събитията.
Както вече бе посочено, понятието за вероятност на събитие е дефиниран за масови явления или по-точно, за хомогенни насипни операции. Хомогенната маса операция се състои от множество повторения на такава единица между операции, или като споменатата тест. Всеки отделен тест е, че той създава определен набор от условия от съществено значение за това насипно състояние на работа. По принцип трябва да е възможно да се възпроизведе съвкупността от условията на неограничен брой пъти. Пример 1. При хвърляне "произволни" зарове само важно условие е, че костта се изхвърля върху масата, и всички други условия (начална скорост, налягане на въздуха и температура, и така оцветяване сечение. Г.) не са взети под внимание. ПРИМЕР 2 стрелецът многократно пожари при определена мишена с дадено разстояние от позицията на "постоянни"; всеки един изстрел е пробна експлоатация в средствата за масова стрелба в тези условия. Ако стрелката е разрешено за различни снимки, за да променя позицията си ( "стои", "лъжа", "коляно"), а след това по-горе условия се променят значително и трябва да говорят за операции на маса стрелба с дадено разстояние. Възможни резултати от една операция или тестване S. наречен случайни събития. Случайни събитие - това е събитие, което може да се случи, или не може да се случи, когато се изпитват S. Вместо "Ела" също да кажете "да дойде", "се появи", "настъпи". По този начин, когато се хвърлят зарове случайни събития са: загуба на определен брой точки, които попадат нечетен брой точки, които попадат брой точки е не по-голяма от три, и т.н. Когато стрелят произволно събитие е да се постигне целта (стрели може или да достигне целта, така че .. и г-ца), срещу него случайно събитие е грешка. Този пример ясно показва, че понятието за случайни събития в теорията на вероятностите не трябва да се разбира в ежедневния смисъл на думата, "това е чиста случайност", тъй като за добър стрелка удря целта е по-скоро правило, отколкото нещастен случай, разбира в обичайния смисъл на думата. Да предположим, че за някои номер н проучвания на събитието A настъпили м пъти, т.е. резултати м една операция са били "успешно", в смисъл, че ние се интересуваме от А реализирани на събитието, както и резултатите от п-M са били "неуспешни" - .. не е настъпило събитие. Определение 1. Съотношението на броя на "успех" изход на броя на тестове, т.е.. Е., Nazyvaetsyachastostyu sobytiyaA. За хомогенна маса операции относителната честота държи стабилно, в смисъл, че ако А събитие появи М1 пъти когато n1 тест (тест една серия), m2 пъти когато N2 изпитвания (тест друга серия), m3 момента n3 и т. Г. относителната честота
леко се отклонява от определен брой р и отклонението, най-общо казано, колкото по-малък, толкова по-тествани. Този номер стр се нарича вероятността на събитие за дадена маса и експлоатацията означена с Р (A):
По този начин, той може да бъде определен като вероятността, наречена статистика. Определяне 2.Veroyatnostyu събития А, или вероятност за "добър" изход единица операция се нарича средната стойност на относителната честота, т.е.. Е. средната стойност на съотношението "успешен" на броя на резултатите на всички единични операции, провеждани (тест). От само себе си се разбира, че ако вероятността на дадено събитие е тестът за N събитие А може да се случи повече от м пъти, а по-малко от м пъти; е само средно настъпва м пъти и по-голямата част от серия от тестове п брой случаи на А ще бъде близо до м. особено ако п - голям. Така veroyatnostP (А) има постоянен брой между нула и единица: