Площта на равностранен триъгълник - формула, пример за изчисление, калкулатор
Равностранен или да се нарече триъгълник, при което всички страни с еднаква дължина, и всичките три ъгъла са равни на 60 °.
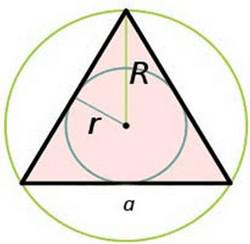
За да намерите един равностранен триъгълник зона може да се използват различни формули.
1. След като отстрани ...
Като се има предвид, че всички страни са равни и да знае дължината им, могат лесно да бъдат намерени на формулата в областта на равностранен триъгълник:
Тази формула е получена от обичайната формула на триъгълника чрез синуса на ъгъла.
Калкулатор равностранен триъгълник квадрата на страната:
A: Площ на триъгълник = 21218
Пример площ изчисление чрез страна на равностранен триъгълник.
Проблем: даден равностранен триъгълник със страни а = 5 см Намерете района.
решение:
площ на триъгълник е равен на 10,6 квадратни сантиметра
2.Cherez ограничена кръг ...
Възможно е да се намери стойността на радиуса на описаните окръжности. Той може да се прилага условия или изчислява въз основа на радиуса на вписан кръг с горната формула:
Square калкулатор равностранен триъгълник на радиуса на описаните окръжности:
Радиусът на описаните окръжности =
A: Площ на триъгълник = 10,000
2.Cherez вписан кръг ...
Налице е също така установяване на формула квадрата на радиуса на вписан кръг.
Вземем примера на изчисляване на площта на равностранен триъгълник над вписан кръг.
Задача. даден правоъгълен триъгълник, който е вписан в окръжност. Странични а = 4 cm, радиусът R = 2,5 cm. Изчислява квадрата на радиуса на окръжност кръг.
Решение. Вече знаем, че радиусът на кръга, два пъти радиуса на вписан. Намерете го:
Сега замени стойността намери във формулата:
Ние считаме, че площта на триъгълник е равен на 32.9 квадратни метра. виждам
- Районът на равнобедрен триъгълник

- Площта на триъгълник от три страни

- Площта на триъгълника чрез синуса и косинуса

- Площта на триъгълника от радиуса на вписан в

- формула на Херон за района на триъгълник
