Как да намерите областта на шестоъгълника

Пишем формулата. Тъй редовен шестоъгълник включва шест равностранни триъгълници, формулата е оформен с формула намери равностранен триъгълник площ: Площ = (3√3 и 2) / 2, където а - страничен дължина на правилен шестоъгълник. [1]

Определяне на една дължина страна. Ако знаем, че дължината на страната, а след това просто да го напиша. В нашия случай, дължината на страната. - 9 см Ако дължината страна не е известна, но известен периметър или Апотема (височината на равностранен триъгълник в шест перпендикулярно страна), е възможно да се намери и на дължината на страната. Ето как се прави:

• Ако знаете периметъра, а след това просто да го разделим на 6 и получаване на дължината на страната. Ако, например, по периметъра - 54 см, а след това се разделят 54 от 6 получаваме 9 cm дължина на страната.

Ако само Апотема известно, дължината на страната може да се изчисли чрез заместване apofemu в формула а = x√3 и след умножаване на отговор от 2. Това е така, защото Апотема е страничен образува x√3 е триъгълник с ъгли 30-60-90 градуса. Ако, например, Апотема - 10√3, тогава х - 10 и дължината страна е равен на 10 * 2 или 20.

Замени стойността на дължината страна във формулата. Просто замени 9 към оригиналната формула. Получават: площ = (3√3 х 02 септември) / 2

Опростяване на отговора. Ние решаваме уравнението и пише отговора. Отговорът трябва да бъде посочен в квадратни единици, тъй като ние се занимаваме с площ. Ето как се прави:

• (3√3 х 02 септември) / 2 =
• (3√3 х 81) / 2 =
• (243√3) / 2 =
• 420.8 / 2 =
• 210.4 cm 2

Apofemu използват за намиране на периметъра. Апотема перпендикулярна на страната на шестоъгълника и създава триъгълник с ъгли 30-60-90. Страните на триъгълника съответстват на пропорциите на х-x√3-2x, където страната на късата страна, разположена срещу ъгъл от 30 градуса, за която х, дължината на дългата страна, разположена срещу ъгъл от 60 градуса, представено x√3 и хипотенузата е представена 2x. [3]

• Апотема - страна представени x√3. Така apofemu заместител в формула а = x√3 и решаване. Ако, например, дължината на Апотема - 5√3, заместителят е число във формулата и получаване 5√3 см = x√3, или х = 5 cm.
• Решаването чрез х, ние открихме, дължина на късата страна на триъгълника. - 5 см Тази дължина е половината от дължината на шестоъгълника. Произведението на 5 от 2 получаваме 10 cm дължина на страната.
• Смята се, че от страна на дължината - 10, умножете това число от 6 и получи периметъра на шестоъгълника. 10 см х 60 см = 6.

Заместването на всички известни данни във формулата. Най-трудното нещо - да се намери периметъра. Сега ние просто трябва да apofemu и периметър замени във формулата и решаване:

• Площ = 1/2 х обиколка х apofemu
• Площ = 1/2 х 60 см х 5√3 cm

Ние се опрости отговора, докато ние се отървете от корен квадратен. Окончателният отговор се дава в квадратни единици.

• 1/2 х 60 см х 5√3 см =
• 30 см х 5√3 =
• 150√3 см =
• 259. 8 cm2

Запишете координатите на всички върхове по осите х и у. Ако знаете, че в началото на шестоъгълника, ние първо трябва да се направи таблица с две колони и седем реда. Всеки ред ще се нарича по име от един от шест точки (точка А, точка Б, точка С, и т.н.), всяка колона се нарича x- или у, координати на точки, отговарящи на тези оси. Запишете координатите на точка А на х и у оси на правото на точката координати на точка в - правото на точка В, и т.н. В долната част, въведете отново координатите на първата точка. Например да кажем, че ние се занимаваме с следните точки, във формата на (X, Y): [4]

• A: (4, 10)
• В: (9, 7)
• С: (11 2)
• D: (2, 2)
• Е: (1, 5)
• F: (4, 7)
• А (отново): (4, 10)

Размножава координатите на всяка точка по оста х у оста на координати за следващата точка. Това може да бъде представен, както следва: прекарваме диагонал надолу и надясно от всяка позиция по оста х. Запишете резултата от дясно на масата. След това ги добавете.

• 4 х 7 = 28
• 9 х 2 = 18
• 11 х 2 = 22
• 2 х 5 = 10
• 1 х 7 = 7
• 4 х 10 = 40
• 28 + 18 + 22 + 10 + 7 + 40 = 125

Размножава координатите на всяка точка по оста у координати на оста х следващата точка. Това може да бъде представен, както следва: прекарваме диагонал надолу и от ляво на всяка координата по оста у. Умножаване всички координатите възлизат на резултатите.

• 10 х 9 = 90
• 7 х 11 = 77
• 2 х 2 = 4
• 2 х 1 = 2
• 5 х 4 = 20
• 7 х 4 = 28
• 90 + 77 + 4 + 2 + 20 + 28 = 221

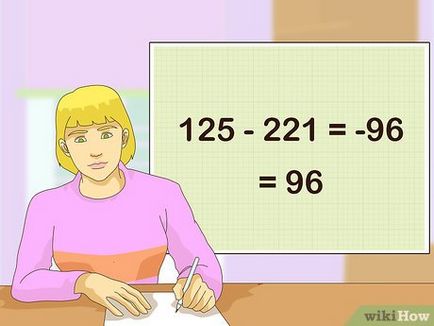
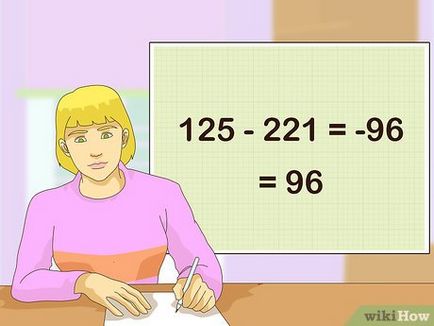
Ние извади сумата от първите координати на втората координира сумата. Ние се изважда 221 от 125, и да получите -96. И така, отговорът е 96, районът може да бъде само положителен.

Ние разделяме разликата от две. Разделете 96 от 2 и да получите областта на неправилен шестоъгълник. Окончателният отговор е 48 квадратни единици.

Метод 4 от 4:
Други начини за намиране областта на неправилен шестоъгълник Редактиране

Намерете лицето на правилен шестоъгълник с липсваща триъгълник. Ако ние сме изправени пред един правилен шестоъгълник, който не разполага с един или повече триъгълници, първият намерите на площ, като че ли цялото. След това намерете областта на "липсващите" триъгълник, тя се изважда от общата площ, и да получите площ налични данни.

• Например, ако се установи, че областта на равностранен триъгълник - 60 cm 2 и областта на липсващата триъгълник - 10 cm 2 е 60 cm 2 - 10 cm 2 = 50 cm 2.
• Ако знаете, че не разполага с точно един триъгълник в шестоъгълник, площта му може да се намери, като се умножи общата площ на 5/6, тъй като ние имаме 5 и 6 триъгълници. Ако не разполагате с достатъчно на двата триъгълника, а след това се умножи по 4/6 (2/3), и т.н.

Разделете неправилен шестоъгълник на триъгълници. Намерете областта на триъгълници и да ги откаже. В зависимост от наличните данни, има много начини да намерите областта на триъгълник.

Потърсете неправилен шестоъгълник някои други фигури: триъгълници, правоъгълници, квадрати. Намерете областта на шестоъгълни форми и да ги откаже.

• Един вид на неправилен шестоъгълник се състои от две или успоредник. За да ги намерите, просто умножете базовата площ от височината и след това сгънете техния район.