Броят на модулите

chislaa модул - е разстоянието от произхода до точката А (а).

За да се разбере това определение заместваме променливата на произволен брой, като например 3 и се опитват да я прочетете отново:

Модул номер 3 - е разстоянието от произхода до точка А (3).

Става ясно, че модулът е нищо друго освен обичайното разстояние. Нека се опитаме да видите разстоянието от началото до точка А (3)

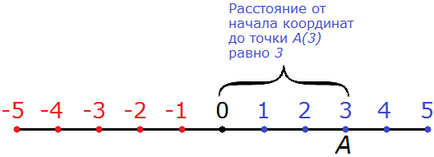
Разстояние от произхода на точка А (3), се равнява на 3 (три единици или три стъпки).

Модул на две вертикални линии показва, например:

номер 3 единица се посочва по следния начин: | 3 |

Модул номер 4 е показан като това: | 4 |

5 на модула е показан като това: | 5 |

Търсехме номера на модула 3 и е установено, че тя е равна на 3. Така че ние напишете:

В него е записано като "модул номер три е три"

Сега ще се опитаме да намерим брой модул -3. Отново се връща на определението и вмъква броя -3. Само вместо да използват нова точка А точка Б. точка А ние вече се използва в първия пример.

-3 брой модул, наречен разстоянието от произхода до точка Б (-3).

Разстоянието от една точка до друга, не може да бъде отрицателна. Ето защо, абсолютната стойност на всяко отрицателно число, като разстоянието няма да е твърде отрицателна. -3 брой модул е ​​броят 3. разстоянието от произхода до точка Б (-3) е равно на три единици:

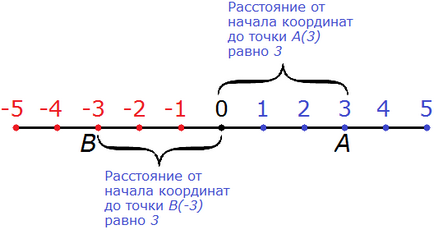
Прочетете като "брой модул минус три е три"

Модул номер 0 е 0, че точката с координира 0 е произход, т.е. разстоянието от произхода до точка о (0) е равна на нула:

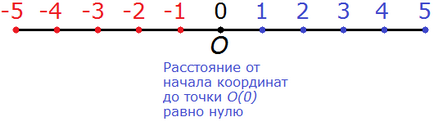
"Модул нула нула"

• брой модул не може да бъде отрицателна;
• За положително число и е равна на нула номера на модула, а за отрицателни - добавка обратен;
• Противоположни числа имат равни модули.

добавка обратен

Номерата, които се различават само по признаци, наречени обратното. Например, номер 2 и 2 са противоположни. Те се различават само в героите. В брой -2 знак минус, а при 2 знак плюс, но ние не виждаме, защото е плюс, както казахме по-рано, не пишете на традицията.

Още примери противоположни номера:

Противоположни числа имат равни модули. Например, за да намерите най-модули 2 и 2

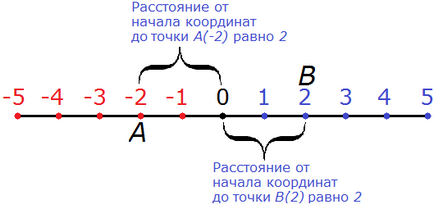
Фигурата показва, че разстоянието от произхода до букви А (-2) и В (2) са еднакво равна на два етапа.

Подобно на урока?
Присъединете се към нашата нова група Vkontakte и започнете да получавате известия за нови уроци