Брои в разделителна компютър, видове, примери за приложение

Брои в компютър метод за определяне на взаимоотношенията са комбинирани елементи. Това са основните обекти на изследване в теория на графите.

основни дефиниции

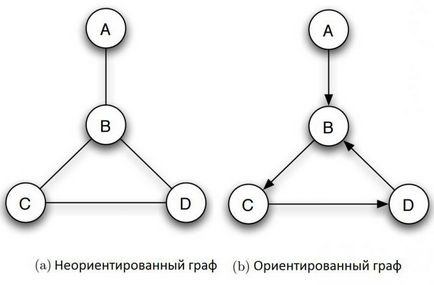
Какво е в графиката по компютърни науки? Той включва множество предмети наречените възли или върхове, някои двойки от които са свързани с т. Н. ребра. Например, графиката на фигурата (а) се състои от четири възли, означен А, В, С и D, B на който е свързан с всеки от другите три върховете ребра, и С и D са свързани. Две възли са съседни, ако те са свързани с предимство. Цифрата показва типичен начин за това как да се изгради графики в компютърните науки. Кръгчета представят върховете и линиите, свързващи всяка двойка от тях, са ребрата.

Какво ненасочена графика се нарича по компютърни науки? Той отношенията между двата края на ребрата са симетрични. Rib просто ги свързва един с друг. В много случаи, обаче, е необходимо да се изрази асиметричен връзка - например, че точки за В, но не и обратно. Тази цел е определянето на графиката в компютъра, все още се състои от набор от възли с набор от насочени ръбове. Всяка ориентирани ръб е връзката между върховете, чиято посока има значение. Целеви графики изобразяват, както е показано на Фигура (Ь), краищата им са представени със стрелки. Когато искате да се подчертае, че индиректно графика, тя се нарича ненасочена.

мрежови модели

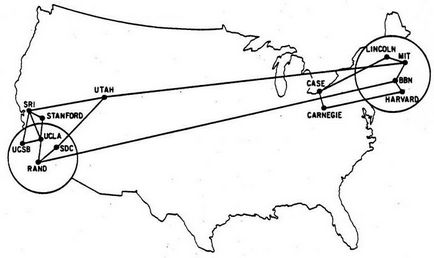
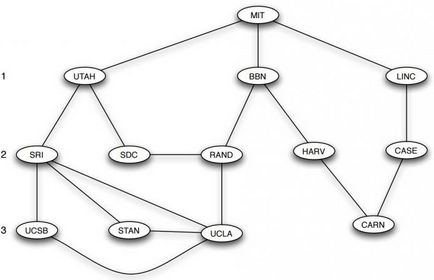
Приложение на графиките в компютъра ви позволява да видите как стоят нещата физически или логически свързани помежду си в мрежова структура. 13-възел ARPANET е пример за комуникационна мрежа, в която най-добрите компютри или други устройства могат да предават съобщения, както и ръбовете представляват пряка връзка, на която информацията може да се предава.

Тази идея мотивира определението на маршрута като серия от възли, свързани от ръбове. Понякога е необходимо да се разгледа по маршрута, който не съдържа само компоненти, но и последователността на краищата ги свързва. Например, последователността на върховете MIT, BBN, RAND, UCLA е маршрут в ARPANET интернет графика. Преминаването на възли и ръбове може да се повтори. Например, SRI, STAN, UCLA, SRI, Юта, MIT е също маршрут. Начинът, по който ребрата не се повтарят, наречена верига. Ако възлите не се повтарят, то се нарича проста верига.

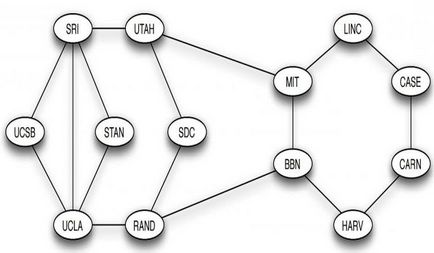
Особено важни видове в компютърни графики - то цикли, които представляват пръстенна структура, като последователност от възли LINC, СЛУЧАЙ, CARN, Харв, BBN, MIT, LINC. Маршрути с най-малко три ребра, при което първата и последната възел са еднакви, а останалата част са различни, представляват циклични графики в компютър науката.

Примери: SRI цикъл, STAN, UCLA, SRI е най-краткия и SRI, STAN, UCLA, RAND, BBN, Юта, SRI значително по-голяма.

Connected графика: разделителна способност (компютърни науки)

Естествено е да се чудя дали е възможно от всеки възел да стигнем до всеки друг възел. Графиката е свързан ако има път между всяка двойка на върховете. Например, ARPANET мрежа - свързан графика. Същото може да се каже и за по-голямата част от комуникационни и транспортни мрежи, като тяхната цел е да насочи трафик от един възел към друг.

елементи

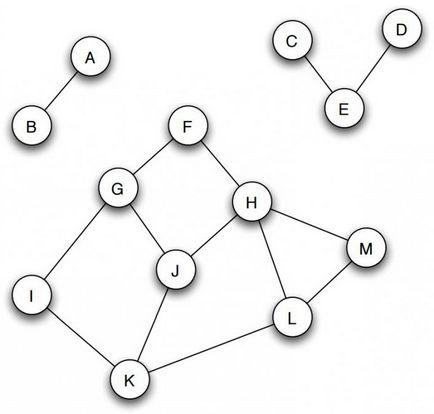
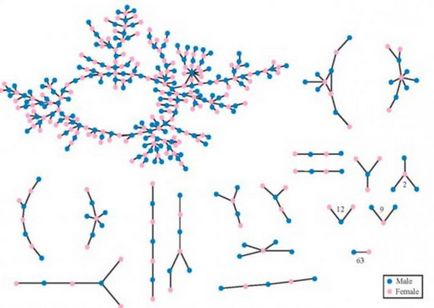
Ако колоната не е свързан към компютъра, те естествено попадат в набор от свързани фрагменти, групи от възли, които са изолирани и не се пресичат. Например, фигура показва три такива части: първата - А и В, а вторият - С, D и Е, и третият състои от останалите върховете.

Компоненти на графиката представляват подгрупа от възли, в които:

• всеки връх подгрупа има маршрут към друг;
• подгрупа не е част от по-голям комплект, в който всеки възел има маршрут към друг.

Когато графиките в компютър се разделят на техните компоненти, това е само първоначалното описание на метода на тяхната структура. Този компонент може да бъде богата на вътрешната структура, важно е за тълкуване на мрежата. Например, официално метода за определяне на важност възел е да се определи колко части ще бъде разделена на броя, ако възелът се отстранява.

Максимална компонент

Дали е свързано? Вероятно не. Свързаност - доста крехка собственост, както и поведението на един възел (или малък набор от тях) може да се сведе до нищо. Например, един човек, без живи приятели е компонент се състои от един-единствен връх, и по тази причина, графът няма да има връзка. Или отдалечен тропически остров, състояща се от хора, които нямат контакт с външния свят, също ще бъде една малка част от мрежата, което потвърждава своята непоследователност.

Глобална мрежа от приятели

Но има и нещо друго. Например, един четец на популярната книга има приятели, които са израснали в други страни, и ги прави един от компонентите. Ако вземем под внимание от родителите на тези приятели и техните приятели, всички тези хора са в една и съща компонент, въпреки че никога не са чували за читателя, говорят на различен език, а до него никога не е било. По този начин, въпреки че световната мрежа на приятелство - не е свързан, читателят ще бъде включен в компонента са много големи, проникваща до всички части на света, която включва хора от най-различни среди и, всъщност, съдържа значителна част от населението на света.

Същото се случва в масивите от данни мрежа - големи и сложни мрежи често имат максимален компонент, който включва значителна част от всички възли. Освен това, когато мрежата включва максимален компонент, тя почти винаги е само една. За да разберете защо, необходимо е да се върнем към примера с глобална мрежа от приятелство и да се опитаме да си представим съществуването на две максимални компонента, всеки от които включва милиони хора. Тя трябва да има един борд на някои от първия компонент на втория максималните два компонента се сляха в едно. Тъй като само един ръб, в повечето случаи това е малко вероятно, че тя не е създадена, и по този начин максимално два компонента в реални мрежи никога не се наблюдават.

В някои редки случаи, когато двата компонента на максимално съвместно съществува от дълго време в истинска мрежа, техният съюз е било неочаквано, драматични, и в крайна сметка да доведе до катастрофални последици.

Злополука сливане компонент

American High School

Разстояние и обхождане в ширина

В допълнение към информацията за това дали две възли са свързани маршрут, теория на графите по компютърни науки дава възможност да се запознаят с неговата дължина - в транспорта, комуникациите и разпространение на новини и заболявания, както и дали тя преминава през няколко върхове или многократно.

За тази цел се определи дължината на маршрут равен на броя на стъпките, че съдържа от началото до края, т.е.. Е. Броят на ръбовете в последователността, която е. Например, Масачузетския технологичен институт, BBN, RAND, UCLA маршрут е с дължина 3 и Масачузетския технологичен институт, Юта - 1. С помощта на дължината на пътя, можем да кажем, че ако две възли са разположени в колоната близо един до друг или далеч разстояние между двата върха се определя като дължината на най-краткия път между тях. Например, разстоянието между Линкълн и SRI е 3, обаче, да се гарантира това, че е необходимо да се провери отсъствието на дължина, равна на 1 или 2, между тях.

Обхождане в ширина алгоритъм

За малка графика разстояние между две възли изчисляват лесно. Но за комплекс има нужда от систематичен метод за определяне на разстояния.

Най-естественият начин да се направи това, и следователно най-ефективните е следният (например глобална мрежа от приятели):

• Всички приятели са обявени намира на разстояние 1.
• Всички приятели на приятели (без да се брои вече споменатите) са обявени на разстояние 2.
• Всички техни приятели (отново, ако не броим етикетирани хората), обявени за дистанционно разстояние 3.

Продължавайки по този начин, търсенето се извършва в следващите слоеве, всеки от които - на устройството на предишния. Всеки нов слой се състои от възли, които не са участвали в предишните, и които попадат ръб от върха на предишния слой.

Тази техника се нарича обхождане в ширина, тъй като тя търси колоната от началния възел, на първо място, обхващащи следващия. В допълнение към предоставянето на метод за определяне на разстоянията, тя може да служи като полезен концептуална рамка за организиране на структурата на графика, както и как да се изгради графика на компютър, с пикове на базата на техния разстояние от фиксирана отправна точка.

Обхождане в ширина може да се прилага не само към мрежа от приятели, но също така и да е графика.

Ако се върнем към глобална мрежа от приятели, можете да видите, че аргументът, който обяснява, принадлежащ към максимална компонент наистина одобрява нещо повече: не само читателят има маршрути до приятели, които да го свързват с една значителна част от населението на света, но тези маршрути са изненадващо кратки ,

Тази идея се нарича "малък свят явлението": светът изглежда малък, ако се замислите какво кратък маршрут свързва някакви двама души.

Сред 64-те вериги, които са достигнали целта, средната продължителност е шест, потвърждаващо броя на име две десетилетия по-рано в игра Dzhona Гера заглавие.