Алгоритми и структури от данни за начинаещи сортиране

В тази част, се вгледаме в пет основни алгоритми за сортиране на данни в масива. Да започнем с най-простото - балон вид - и да завърши "бърз вид» (бързасортировка).
За всеки алгоритъм, в допълнение към обяснение на работата си, ние също така посочват, паметта му и сложността на времето в най-лошия, най-добре и за общия случай.
метод Swap
За опростяване на кода и подобри четливостта ще се въведе метод Swap. която ще замени стойностите в масива от индекс.
Bubble вид - е най-лесният за сортиране алгоритъм. Тя преминава през масива няколко пъти, на всеки етап от преместване на най-важната от несортиран края на масива.
Например, ние имаме масив от цели числа:
Първият преминаването през масива, ние сравняваме стойностите на 3 и 7. От 7 е по-голяма от 3, ние ги оставят такива, каквито са. След това сравнете 7 и 4. 4 е по-малко от 7, така че ние ги подредите чрез плъзгане седем една позиция по-близо до края на масива. Сега тя изглежда така:
Този процес се повтаря в продължение на толкова дълго, колкото седем няма да дойде, докато почти до края на масива. В края той се сравнява с елемент 8, който е по-голям, и по този начин не е споделяне. След като обиколи масива веднъж, тя изглежда така:
Както е направена най-малко един обмен на ценности, ние трябва да мине през масива отново. В резултат на този пасаж, ние се движат към мястото на номер 6.
И там отново е произведен най-малко един обмен, и по този начин да премине през масива отново.
Следващият пасаж обмен не е направено, което означава, че нашата гама се сортира и алгоритъмът завърши своята работа.
Вмъкването на сортиране работи, минаваща през масива и преместване на желаната стойност в началото на масива. След обработването на следващата позиция, ние знаем, че всички елементи, преди да го подредени, а след това - не.
Важен момент: вмъкване на сортиране третира елементите на масива в ред. Тъй като алгоритъмът работи на елементите от ляво на дясно, знаем, че всичко, което е останало от текущия индекс - вече сортиран. На тази фигура е показан като част от увеличава масив сортирани с всеки подаване:
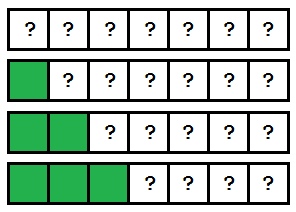
Постепенно сортира част на масива расте, и в крайна сметка, на масива ще се нареди.
Нека да разгледаме конкретен пример. Ето ни неподреден масив, който ние ще използваме:
Алгоритъмът започва с индекс стойност 0 и 3. Тъй като това е първият индекс на масива, преди да се счита за приобщаващ сортиран.
На следващо място, ние се обръщаме към броя 7. От 7 е по-голям от всяка стойност в сортират части, се пристъпва към следващия елемент.
На този етап елементите с индекси 0..1 са сортирани, а за елементите с индекси не 2..N известни.
Трябва да се провери стойността на 4. Тъй като е по-малко от седем, ние трябва да го премести в правилната позиция в сортирания част на масива. Остава открит въпросът как да го определят? Това се постига чрез FindInsertionIndex. Той сравнява стойността, предавана към нея (4), като всяка стойност в сортирано част, докато намери място, за да вмъкнете.
Така че ние открихме, индексът 1 (стойности между 3 и 7). метод Insert извършва вмъкване, премахване на вложка стойност на масива, и измества всички стойности от индекса, за да вмъкнете, нали. Сега масива изглежда така:
Сега част на масива, като се започва от нула и завършва с елемент елемент с индекс 2 се сортират. Следваща пасаж започва с индекса 3 и 4. Тъй като стойността на алгоритъма, ние продължаваме да се направи такова вмъкване.
Когато няма повече място за вложки, масивът се смята за напълно подредени и алгоритъма е завършен.
Избор Сортирайте - това е хибрид между балона и сортиране чрез вмъкване. Подобно нещо на балона, алгоритъмът преминава през масива отново и отново, движещи се една стойност в правилната позиция. Въпреки това, за разлика от сорта на балона, той избира най-малката стойност, вместо максималната несортиран. Както и при поставяне на сортиране, подредена част на масива се намира в началото, а в подобно на балон, тя е в края.
Нека да разгледаме работата на сортирането в нашата селекция от несортиран масив.
През първото преминаване през алгоритъма FindIndexOfSmallestFromIndex метод се опитва да намери най-малката стойност в масива и да го придвижи към върха.
Като такъв малък масив, можем да кажем веднага, че най-ниската стойност - 3, и тя вече е в правилната позиция. На този етап ние знаем, че първата позиция в масив (индекс 0) е най-малката стойност, поради това, в началото на масива вече е сортиран. Ето защо, ние започваме второто преминаване - този път в индексите от 1 до п - 1.
На втория проход, като установим, че най-малката стойност - 4. Ние се промени мястото си с втория елемент, седем, а след това 4 се издига в правилно положение.
Сега несортиран част на масива започва от индекс 2. Тя расте от един елемент, всеки път, чрез алгоритъма. Ако на всеки пасаж, ние не са направили някоя борса, което означава, че масивът е сортиран.
След два паса алгоритъмът спира:
Разделяй и владей
До момента имаме счита линейни алгоритми. Те използват малко повече памет, но е с квадратно сложност. На примера на сливането на сортиране алгоритъм, ние гледаме на типа на "разделяй и владей" (разделяй и владей).
Ако искате да намерите човек, на име Петров, че няма да се търси, като се започне с буквата А и превръщането на една страница. Възможно е да се открие една книга някъде. Ако получите писмото T, perelistnete няколко страници назад, може би прекалено много - с буквата А. След това отидете напред. По този начин, обръщане назад и напред, всички по-малко от вас страници в крайна сметка ще намерят най-подходящия.
Колко ефективни са тези алгоритми?
слеят Сортирайте
Когато сортиране чрез сливане ние разделяме масива на половина толкова дълго, колкото всяка секция няма да бъде един от елементите дълго. След това тези области обратно на мястото му (слее) в правилния ред.
Нека да разгледаме масив:
Разделя се на две:
И ние ще се разделим всяка част на половина, докато тя ще остане част от един елемент:
Сега, когато сме разделени от порядъка на най-кратките възможни области ние ги обедините в правилния ред.

На първо място, ние се групи от по две сортиран елемент, тогава ги "събират" в групи от по четири елемента и в края на краищата се съберат всички заедно в сортиран масив.
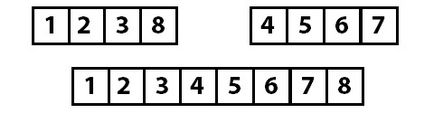
За нас алгоритъм трябва да изпълни следните операции:
- Операцията за рекурсивно разделяне на масива в групи (сортиране метод).
- Сливанията в правилния ред (Merge метод).
Заслужава да се отбележи, че за разлика линейните алгоритми за сортиране, сортиране чрез сливане е да се разделят и снаждане масив, независимо от това дали тя е била първоначално или не сортирани. Ето защо, независимо от факта, че в най-лошия случай тя ще работи по-бързо от линеен, в най-добрия, изпълнението му ще бъде по-ниска, отколкото в линия. Ето защо, по обединяване нещо - не най-доброто решение, когато трябва да се справи със масив частично uporyadchenny.
обществени невалидни Sort (T [] елемента)
ако (leftIndex GT; = Ляв. Дължина)
елементи [targetIndex] = десен [rightIndex ++];
иначе, ако (rightIndex GT; = Десен. Дължина)
елементи [targetIndex] = оставени [leftIndex ++];
иначе, ако (вляво [leftIndex]. CompareTo (вдясно [rightIndex]) LT; 0)
елементи [targetIndex] = оставени [leftIndex ++];
елементи [targetIndex] = десен [rightIndex ++];
Quicksort
Бързо сортиране - е друг алгоритъм, като "разделяй и владей". Тя работи чрез рекурсивно повтарят следните стъпки:
- Изберете указател на ключ и го разделете на масива на две части. Това може да стане по различни начини, но в тази статия ние използваме произволен номер.
- Преместете всички елементи на ключа от дясната страна на масива, и всички елементи, е по-малко от ключа - на ляво. Сега, ключовият елемент е в правилната позиция - това повече от който и да е елемент от ляво и долния десен ъгъл на всеки елемент.
- Повторете първите две стъпки, докато масив е напълно подредени.
Нека да разгледаме алгоритъма на следващата масива:
Първо, ние избира произволно ключов елемент:
Int pivotIndex = _pivotRng. Следваща (вляво прав.);
Сега, когато знаем ключовият индекс (4), ние приемаме стойността на този индекс (6), както и прехвърляне на стойности в масива, така че всички числа по-големи или равни на ключ са от дясната страна, а всички числа е по-малко от ключа - на ляво , Моля, имайте предвид, че по време на трансферната стойност на индекса ключов елемент може да се промени (както ще видим скоро).
Преместване стойности проведени метод дял.
На този етап, ние знаем, че стойността на 6 е от дясната страна. Сега този процес се повтаря в продължение на лявата и дясната страна на масива.
Ние наричаме метод бързасортировка рекурсивно за всяка от частите. Ключов елемент от лявата страна става пет. Когато преместите стойностите тя ще се промени своя индекс. Основното нещо - не забравяйте, че това е важно, че е от ключово значение, а не своя индекс.
Отново се приложи бързо вид:
Оставихме един от несортиран стойност, а защото знаем, че всичко останало е сортиран, алгоритъмът приключва.